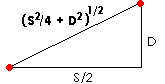Time Dilation

Any device consisting of a regular repetitive motion, can be used as a clock. Lets then consider a clock made out of two mirrors. Separated by a distance "D". A roundtrip of "2D" represents one tick of the clock. 

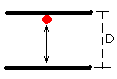    Lets assume that the system is located inside a constant velocity (nonzero) moving train. You are located inside the train and are watching the clock. What you see is the photon bouncing up and down between the two mirrors (see image @ left). Since a round trip is "2D" and the velocity of the photon is "C", we can conclude that the time required for a tick of the clock is Ts=(2D) / (C). A point of this equation is that relative to you, the clock is stationary. (Ts= Time stationary)

 

Lets now assume that while you are inside the train watching the photon bounce up and down, your friend is standing outside the train watching you and the clock pass by (from left to right). What you friend sees is the photon bouncing in a triangular type path between the two mirrors:

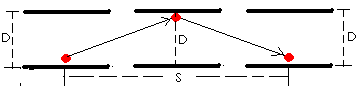
We will supply the train with a velocity of "V". "S" is the horizontal displacement  the system has undergone in one click of the clock (distance train has traveled). Using the Pythagorean theorem , we can solve for the actual distance the photon traveled in one click.

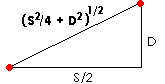
Which implies:

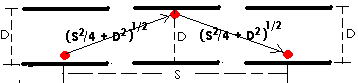
So the actual distance the photon travels is 2(S2/4 + D2)1/2. We also know that the speed of the photon is "C". So we can now formulate "Tm" (Time motion) of the photon viewed from the ground: Tm =  [ 2(S2/4 + D2)1/2 ] / (C)

"Tm" is  in terms of "S" and "D". We know that "S" is the displacement of the system in time "Tm" (One Click), and the velocity of the system at that time is "V", thus: S = V*TM. Substituting this in to our formula for "Tm" yields:

Tm = [ 2{ (V*Tm)2/4 + D2}1/2 ] / (C)

We also know that Ts = (2D)/(C). Rearranging this we get: D = (Ts*C)/(2). Substituting this in for D gives us:

Tm = [ 2{ (V*Tm)2/4 + (Ts*C)2/4}1/2  ]/ (C)

Using a little Algebra, this becomes:

Tm = { (V2Tm2) + (Ts2C2) }1/2 / (C)

Now we have an equation for "Tm" in terms of "V" and "Ts". The goal, is to express the relationship between "Tm" and "Ts" as "V" varies.

Multiplying both sides by "C", then squaring both sides yields:

Tm2C2 = V2Tm2 + Ts2C2

Subtracting V2TM2 from both sides gives:

Tm2C2 - V2Tm2 = Ts2C2

Factoring out Tm2 from the left yields:

Tm2 ( C2 - V2) = Ts2C2

Divide both sides by ( C2 - V2 ) gives:

Tm2 = Ts2C2 / ( C2 - V2) 

Now we have a relationship between "Tm" and "Ts" that is only dependent upon the velocity of the system. This equation, in itself, can explain Time Dilation. But to make it a little more obvious, lets algebraically manipulate the equation.

In the fraction on the left., multiply it by (1/C2) / (1/C2). This is permissible because we are multiplying the left side by 1;  (1/C2)/(1/C2) = 1. Numerator time numerator and denominator times denominator gives:

Tm2 = (Ts2C2/C2) / ( (C2 - V2)/C2 )

which simplifies to:

Tm2 = Ts2 / [ 1- (V2/C2) ]

now raise both sides to the 1/2 power:

Tm = Ts / [ 1- (V2/C2) ]1/2

This is the defining equation of "simple" Time Dilation. This equation reveals that given a measurement of time from inside a constant velocity system, one can compute the the measurement of time from outside the system (and vise versa), given that one know the relative velocity of the outside observer to the system. (that's a mouthful)

Using a little numerical analysis, we can conclude some know and unknown (time dilation) consequences of Einstein's Relativity.

Tm = Ts / [ 1- (V2/C2) ]1/2

If we let the velocity of the system "V" equal zero, then in the denominator V2/C2  equals zero and 1- 0 equals 1. The square root of 1 is 1 and Tm = Ts/1 = Ts. So we end up with Tm = Ts. Which is what we expect. If the train is not moving (relative to the two observers), then no time dilation will take place.

Tm = Ts / [ 1- (V2/C2) ]1/2

If we let "V" the velocity of the system be anything between 0 and C, then that number squared over C squared will be a proper fraction (denominator > numerator). The smaller the "V" the smaller the fraction. 1 - (Proper Fraction) will always be between 1 and 0. The square root of numbers between 1 and 0 is always a proper fraction. We now have:

Tm = Ts / (Proper Fraction)

or

(Proper Fraction) * Tm = Ts

The product of a proper fraction and a number will always yield a smaller number than the original. Since the numerator is less than the denominator in the proper fraction, "Tm" is getting divided by more than it is getting multiplied by. For any "V" between 0 and C: Tm>Ts. 

Taking the limit of "Tm = Ts / [ 1- (V2/C2) ]1/2" as V goes to C from the left yields infinity. This also is intuitive if we consider that as the velocity increases, Tm differs from Ts considerably. Also notice that if  V is greater than C gives you get non-real numbers.

Lets solve the "defining" equation for "Ts/Tm":

Ts/Tm = [ 1- (V2/C2) ]1/2

Lets give "C" the value of 3.0 x 10^8 meters per second.

Ts/Tm = [ 1- (V2/(9.0 x 1016)) ]1/2

Notice that if we pick values for "V" drastically smaller than "C" than our "Ratio of Times" (Ts/Tm)is very very close to one. This makes since. At low speeds "Ts" is almost equal to "Tm"

Notice when "V" is 10^8 (223693629 mph) how "Ts/Tm" is only .94, meaning that "Ts"  is 94% of "Tm". This is an extremely high speed, but not much dilation of time occurs. 

Notice now if we let "V" equal 2 x 10^8, our ratio of times is .75, meaning that Ts is 75% of Tm. And if we let "V" equal 2.999 X 10^8, the ratio equals .026, meaning that "Ts" is now 2.6% of "Tm". We can see a trend that as "V" gets larger "Ts" and "Tm" differ greatly, but only @ speeds very close to the speed of light. This explains why even the space shuttle doesn't experience much time dilation, it travels in space @ a mere 7823 meters per second.

 

 

                  -Seth Boudreaux